Chapitre 2 : La musique ou l'art de faire entendre les nombres

TP 1 Notes, intervalles et mathématiques

Objectif : Répondre à la problématique : Comment les mathématiques influent sur l’harmonie des sons

La gamme de Do Majeur

Quand on récite le nom des notes de musique en partant du Do, la huitième note porte à nouveau le nom de Do : Do¹, Ré¹, Mi¹, Fa¹, Sol¹, La¹, Si¹, Do². Entre ces deux notes, il existe donc un intervalle que l’on appelle une octave. La sensation auditive est très proche entre deux notes séparées par une octave, seule la hauteur change : une est plus aiguë que l’autre. La fréquence du Do² (132 Hz) est le double de la valeur du Do¹ (66 Hz)

Au VIème siècle avant J.C, Le mathématicien et philosophe Pythagore (oui, oui, celui du théorème…) voulut percer le secret de l’harmonie musicale. Il a ainsi établi que la fréquence d’une note est inversement proportionnelle à la longueur de l’instrument. Ainsi, la flûte à bec ténor mesure environ 60 cm, la soprano, sonnant une octave au-dessus, mesure environ 30 cm, et le garklein, sonnant une octave au-dessus mesure 15 cm. On peut obtenir les mêmes résultats en comparant la longueur des différents tuyaux d’un orgue.

Selon l’école pythagoricienne, l’harmonie de deux sons joués ensemble s’explique par l’existence de rapports mathématiques entre la hauteur des sons.

Reprenons la gamme de Do Majeur. Elle est constituée de 7 notes séparées par des intervalles. La huitième note est à nouveau le Do, une octave au-dessus.

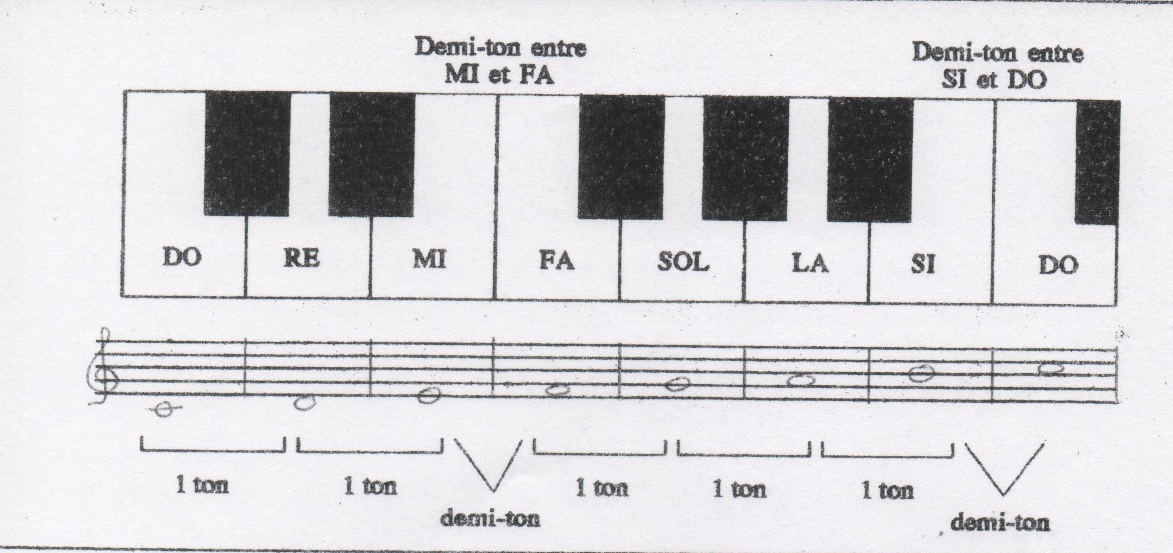
Sur un clavier de piano, cela donne:

On obtient donc 8 notes et sept intervalles.

Si tous les intervalles valent 1 ton, la gamme ne contient plus que 6 notes, la septième étant le Do à l’octave supérieure

Si on joue tous les ½ tons, on obtient 12 notes, la treizième est à nouveau un Do à l’octave supérieure.

Dans la gamme de do majeur, on a donc 12 intervalles d’1/2 ton pour 8 notes. La gamme majeure peut donc être divisée de cette manière :

Do¹ (+1 ton) ; Ré¹ (+1 ton) ; Mi¹ (+1/2ton) ; Fa¹ (+1 ton) ; Sol¹ (+1 ton) ; La¹ (+1 ton) ; Si¹ (+1/2ton) ; Do²

Pythagore travaillait sur un monocorde, c’est-à-dire un ensemble constitué de deux piquets fixes entre lesquels on tendait une corde. Un chevalet mobile permettait de réduire la longueur de corde vibrante. La corde entière donnait une note de fréquence F⁰.

En plaçant le chevalet au milieu de la corde, on obtenait, de part et d’autre, deux cordes vibrantes de longueurs égales et dont la fréquence F¹ était le double de la fréquence F⁰.

Question : Trouver une équation permettant d’exprimer F¹ en fonction de F⁰, puis Fⁿ en fonction de F⁰

On peut dire que F¹ = 2F⁰. Pour une fréquence Fⁿ alors, Fⁿ = 2n F⁰

En plaçant le chevalet à différents endroits, on obtenait ainsi des notes dont la fréquence dépend du rapport entre la longueur de la portion de corde vibrante et la longueur initiale de la corde.

Nom de l’intervalle	Seconde (Do1/Ré1)	Tierce (Do1/Mi1)	Quarte (Do1/Fa1)	Quinte (Do1/Sol1)	Sixte (Do1/La1)	Septième (Do1/Si1)	Octave (Do1/Do2)
Rapport de fréquence	9/8	5/4	4/3	3/2	5/3	15/8	2/1
Rapport de longueur	8/9	4/5	3/4	2/3	3/5	8/15	1/2

 

Le tableau précédent donne les caractéristiques des intervalles présents dans la gamme de Do Majeur.

Les rapports en rouge sont des épimores, c’est-à-dire des rapports particuliers ou le numérateur est égal au dénominateur + 1. On les obtient naturellement en divisant la longueur de la corde par des entiers.

Sur une échelle de fréquences, additionner ou retrancher des intervalles revient respectivement à multiplier ou diviser leurs rapports de fréquences.

Question : additionnez les intervalles de quarte et de quinte. Que remarquez-vous ?

Question : Faites de même avec les intervalles de tierce et de sixte, puis de seconde et de septième. Pourquoi dit-on que les intervalles justes sont l’octave, la quinte et la quarte ?

L’addition des intervalles de quarte et de quinte nous donne 2/1, soit le rapport observé pour l’octave.

Question : Faites de même avec les intervalles de tierce et de sixte, puis de seconde et de septième. Pourquoi dit-on que les intervalles justes sont l’octave, la quinte et la quarte ?

L’addition des autres intervalles ne permet jamais d’obtenir 2/1 (25/12 pour sixte + tierce et 135/64 pour seconde + septième). Ainsi, seule la quinte + la quarte et l’octave ont des rapports égaux entre eux.

Harmonie, mathématiques et culture

Nos sensations musicales sont déterminées d’une part par l’acoustique et la biologie de notre système auditif et d’autre part par notre culture. On a ainsi, à l’aide de ces deux paramètres, déterminer l’existence de consonances (intervalle qui sonne juste) et de dissonances (intervalle qui sonne faux). Pour les pythagoriciens, les sons consonants sont associés aux rapports de fréquence les plus simples (2/1 ; 3/2 ;…). Au Moyen-Age, seuls ces intervalles étaient autorisés.

L’intervalle de quarte augmenté (auquel on ajoute un ½ ton), ou triton, était réputé convoquer le diable car il semble grincer (Diabolus in musica).

Cet accord a été particulièrement utilisé par le jazz et le rock’n’roll, d’où leur réputation de musique diabolique. Le guitariste Jimi Hendrix (27 novembre 1942-18 septembre 1970) l’a utilisé dans sa chanson Purple Haze.

Quand on écoute l’introduction, on remarque que la basse et la guitare jouent un triton

Question : Si la basse joue un mi, quelle est la note jouée par la guitare pour obtenir un triton ?

La guitare doit jouer un Do pour obtenir un intervalle de 4 ½ ton (quarte = 3ton et ½ ton, quarte augmentée = 4 ton)

Après le solo d’introduction sur une gamme pentatonique (Mi, Sol, La, Si, Ré), le morceau utilise un accord de mi modifié.

L’accord non modifié est l’accord de mi majeur (Mi¹ - Si¹ - Mi² - Sol#² - Si² - Mi³).

L’accord modifié est un mi 7#9 (Mi¹ - Sol#¹ - Si¹ - Ré² - Sol² - Mi³).

Question : indiquez les intervalles présents entre le Mi¹ et les autres notes pour les deux accords. Rappel : le dièse (#) ajoute un 1/2ton.

 

3+1/2 ;6 ;8 ;9 ;12

2 ;3+1/2 ;5 ;7+1/2 ;12

Les deux versions suivantes sont jouées l’une avec le mi majeur, l’autre avec le mi modifié

Question subjective : Quelle est l’impression créée avec l’accord modifié ?

L’accord modifié induit une tension, l’impression qu’il manque quelque chose qui doit être résolu, mais en ajoutant des harmonies.

Lorsque l’on met le tout ensemble :

Nous l’avons vu en travaillant sur la gamme de Do, les intervalles ne sont pas constants entre toutes les notes. Pour pallier à ce problème, on peut altérer les notes en ajoutant (#) ou en retirant (b) un demi-ton.

Ces douze notes constituent la gamme diatonique.

Comment a-t-on pu construire cette gamme de douze notes ?

Pythagore et ses disciples étaient très attachés au concept d’ordre et d’harmonie. Il est donc parti de la corde entière, comme nous l’avons vu, et a proposé d’avancer de quinte en quinte, tout en restant dans l’octave original. Cela parait complexe énoncé ainsi, passons à la pratique :

On part de la corde entière qui vaut 1(Do). La première quinte vaut 3/2 soit 1,5 ce qui correspond au Sol. En avançant d’une quinte, on trouve : 3/2 X 3/2 c’est-à-dire 32/22 soit 2.25. Mais nous sommes au-delà de l’octave (2). On divise la fréquence obtenue par deux pour revenir dans l’octave d’origine et on obtient 1.125 (9/8) soit le Ré. La troisième quinte donne 33/23 soit 3.38. On la ramène dans l’octave en divisant par deux et on obtient le La (1.69 ; 5/3). La quatrième quinte vaut 34/24 soit 5.06. Cette fois encore, on divise par deux mais le résultat (2.53) est encore dans une octave supérieure. On divise à nouveau par deux pour obtenir un résultat compris entre 1 et 2 (l’octave de départ) : 1.256 soit 5/4, le Mi. Au bout de la douzième quinte, on retrouve à peu de choses près la note Do à l’octave supérieur. On parle donc de cycle des quintes. Il suffit ensuite de mettre les notes dans l’ordre des fréquences croissantes.

Complétez le tableau suivant :

Note de base	1	2	3	4	5	6	7	8	9	10	11	12	Nombre de divisions par 2
	Fréquences obtenues par addition des quintes
1	1.5	2.25	3.38	5.06	7.59	11.39	17.09	25.63	38.44	57.67	86.50	12.95	0
		1.13	1.69	2.53	3.8	5.7	8.54	12.81	19.22	28.83	42.25	64.87	1
				1.27	1.9	2.85	4.27	6.41	9.61	14.42	21.62	32.44	2
						1.42	2.14	3.2	4.8	7.21	10.81	16.22	3
							1.07	1.6	2.4	3.60	5.41	8.11	4
									1.2	1.8	2.7	4.05	5
											1.35	2.03	6
Do	Sol	Ré	La	Mi	Si	Fa#	Do#	Sol#	Mib	Si	Fa	Do

 

Mettez dans l’ordre les douze notes de la gamme diatonique

Do, Do#, Ré, Mib, Mi, Fa, Fa#, Sol, Sol#, La, Sib,Si

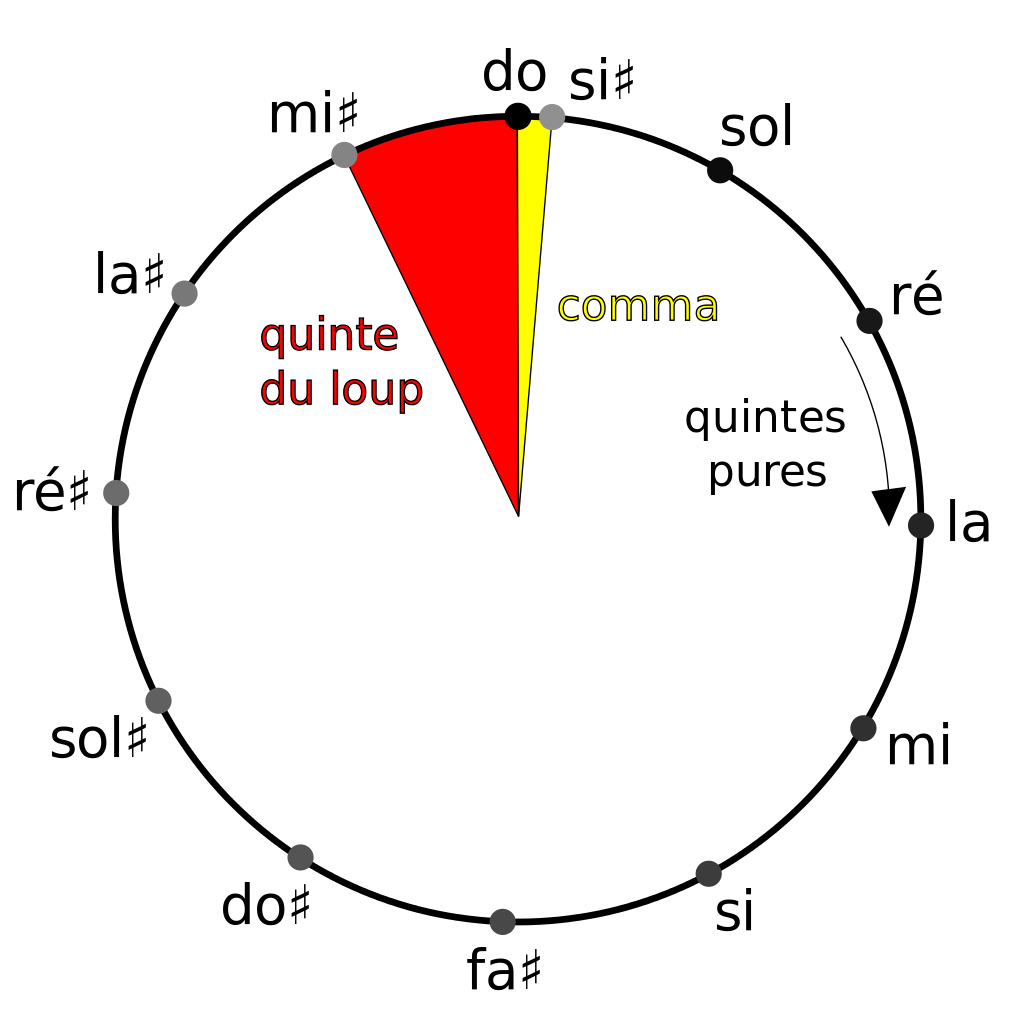
On pourrait jouer à enchainer les quintes à l’infini, mais si on observe bien, la treizième note obtenue après l’addition de douze quintes est très proche de la note initiale. On parle donc de cycle des quintes. Cependant, on obtient 11 quintes justes et une quinte légèrement fausse. Cette quinte est appelée quinte du loup car sa sonorité est discordante et semble « hurler comme un loup ». Vous noterez d’ailleurs l’origine de l’expression « y a un loup », qui signifie qu’il y a quelque chose qui cloche.

Ce cycle des quintes est représenté dans un cercle

 

Que représente le comma sur le cercle ?

Le comma représente le léger intervalle (1/2 ton) en trop au terme des douze quintes.

Pour résoudre le problème, de nombreux musiciens proposent une nouvelle manière de découper la gamme : la gamme tempérée.

Le principe est de séparer une octave en douze intervalles égaux d’un demi ton. On obtiendra ainsi un rapport de fréquence pour le demi ton égal à la racine douzième de 2 : ¹²√2=1.059463094359… Ainsi, en multipliant 12 fois n’importe quel nombre x par cette valeur, on obtient 2x, soit l’octave supérieure.

Calculez la fréquence des douze notes de la gamme tempérée en partant d’une fréquence initiale de 1.

1 ; 1.06 ; 1.12 ; 1.19 ; 1.25 ; 1.33 ; 1.45 ; 1.53 ; 1.63 ; 1.72 ; 1.83 ; 1.93 ; 2

Comparez les fréquences des notes dans les deux gammes.

Do : 1 pour les deux gammes

Ré : 1.07 et 1.06

Mib : 1.13 et 1.12

Mi : 1.20 et 1.19

Fa : 1.35 et 1.33

Fa# : 1.42 et 1.45

Sol : 1.50 et 1.53

Sol# : 1.60 et 1.63

La : 1.69 et 1.72

Sib : 1.80 et 1.83

Si : 1.90 et 1.93

Do :2.03 et 2

En conclusion, aucune quinte n'est tout à fait juste (selon Pythagore), mais on fait disparaître la dernière quinte très dissonnante. Les autres fréquences sont tellement proches que nos oreilles ne perçoivent pas de différence.